Uma abordagem importante, para representação da forma de um objeto, é transformá-la em uma estrutura mais simples, chamada de esqueleto. O esqueleto de um objeto pode ser obtido por meio de diversas técnicas, como transformada de distância, afinamento de objetos entre outras.
Neste artigo, será apresentado como utilizar a morfologia para extração do esqueleto de uma imagem binarizada. Acesse Morfologia Matemática para Processamento de Imagens, para entender sobre erosão e dilatação, operações que são a base dos cálculos apresentados a seguir.
Transformada do eixo-médio
A transformada do eixo-médio, proposto por Blum (1967), determina o conjunto de pontos que estão mais próximos da borda do objeto. De uma maneira formal, o eixo médio de um objeto é composto pelos centros das maiores circunferências que cabem no objeto. A figura 1 ilustra essa definição para um retângulo [PS].
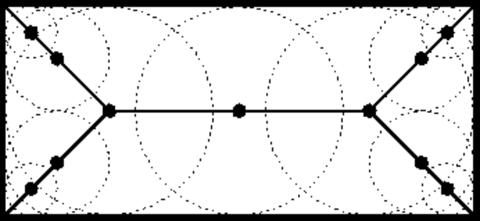
Embora a transformada do eixo médio resulte em um esqueleto aceitável. Sua utilização na prática resulta em um problema em termos computacionais. Tal implementação envolve o cálculo da distância entre cada ponto interior e da borda do objeto. Diversos algoritmos foram propostos para tentar melhorar a eficiência desta transformada [PS].
Outros exemplos de objetos e seu esqueletos são demonstrados na figura 2. Pode-se observar, nas duas primeiras imagens, que objetos e formas diferentes podem ter o mesmo esqueleto.
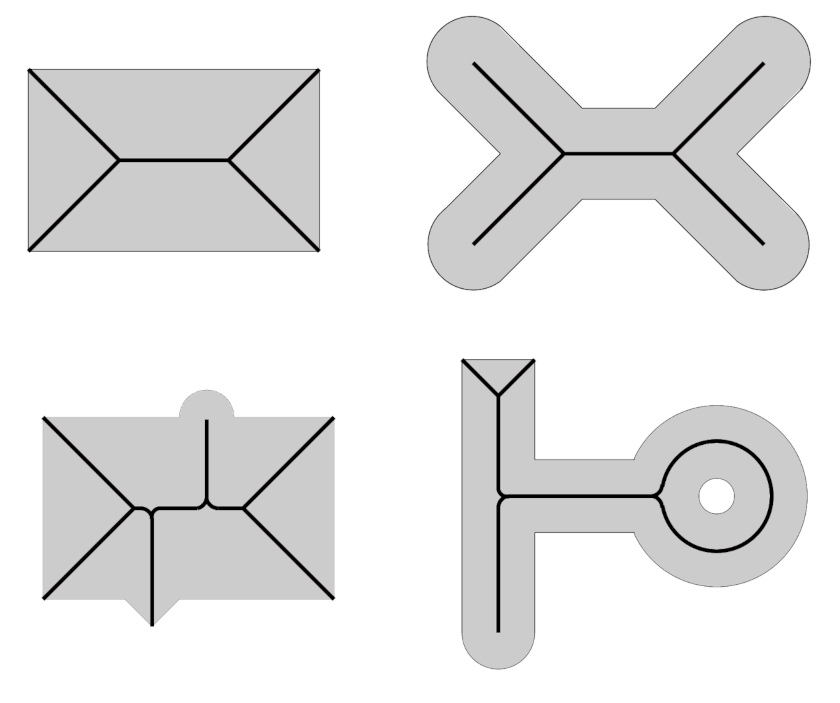
Transformada de distância
A transformada de distância corresponde ao mapa resultante da distância entre cada ponto interior do objeto e de sua borda mais próxima [PS]. Essa transformação depende do tipo de cálculo de distância utilizado.
Um exemplo do processo da transformada de distância é ilustrado na figura 3, o esqueleto do objeto, formado pelos valores mais altos de distância, corresponde às regiões mais claras. O cálculo de distância utilizado é a distância euclidiana.



Na figura 4, é ilustrada uma imagem binária, sua representação da transformada euclidiana e seu esqueleto criado, a partir dos valores mais altos (pontos claros).

Processo de esqueletização com morfologia matemática
A esqueletização de uma imagem binarizada por morfologia, apresentada a seguir, tem como base a transformada de distância. Todo o processo é bem simples, com apenas duas operações morfológicas e uma subtração, encadeadas em um laço é possível extrair o esqueleto.
Observe a imagem binarizada A e o elemento estruturante B, logo abaixo. Nas linhas seguintes, observe que:
- A primeira coluna apresenta a erosão por B da imagem da linha anterior;
- A segunda coluna apresenta a dilatação da imagem da primeira coluna por B. A segunda coluna, também, corresponde a abertura da imagem da primeira coluna da linha anterior;
- A terceira coluna apresenta a subtração da primeira coluna da linha anterior pela segunda.
Por fim, na última linha, a imagem da terceira coluna de título “Resultado” apresentada a soma de todas as imagens da terceira coluna. Observe que essa somatória resultou no esqueleto da imagem retangular A.

Imagem binarizada

Elemento estruturante
Erosão por B
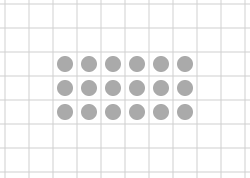
Erosão de A por B
Dilatação da 1ª coluna por B
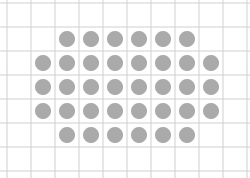
= (A ⊖ B) ⊕ B
Abertura de A por B
Subtração da 1ª coluna da linha anterior pela 2ª coluna
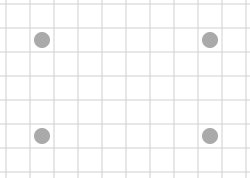
A subtraída pela abertura de A por B
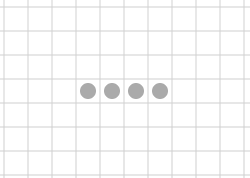
Erosão de A por B duas vezes
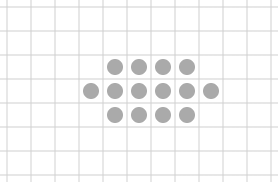
= (A ⊖ B) ⊖ B ⊕ B
Erosão de A por B, seguida da abertura por B
Abertura de A por B
subtraída pela Erosão de A por B

Erosão de A por B três vezes

Erosão de A por B duas vezes, seguida da abertura por B

Abertura de A por B
subtraída pela Erosão de A por B
Exemplos
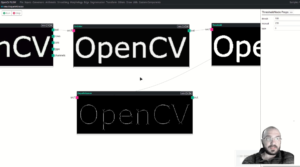
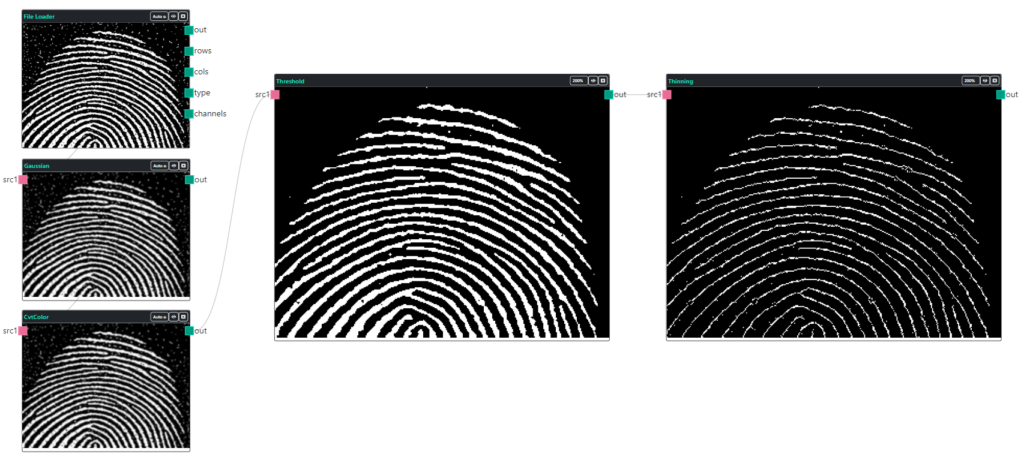
A seguir, duas demonstrações de esqueletização, da palavra “OpenCV” e de uma imagem da digital de um dedo. O processo de extração do esqueleto da Figura 8 é carregar a imagem, suavizar a imagem com o filtro gaussiano, converter em tons de cinza, limiarizar/binarizar a imagem e extrair o esqueleto.


Referências
[PS] Pedrini, H.; Schwartz, W. R.; Análise de Imagens Digitais: Princípios, Algoritmos e Aplicações. Thomson Learning, 2007
[LQ] Li, Quannan et al. “Skeleton Extraction Using SSM of the Distance Transform.” (2008).
[RSA] R. Fisher, S. Perkins, A. Walker and E. Wolfart. Skeletonization/Medial Axis Transform. Acessado em 01/05/2023
[FA] Félix Abecassis – OpenCV – Morphological Skeleton. Acessado em 02/05/2023