Para representar como enxergamos os objetos e o mundo a nossa volta em sistemas computacionais, e então possibilitar que computadores consigam reproduzir de volta estas imagens em seu monitor, ou possibilitar a criação de ferramentas de edição de imagens, ou sistemas que analisam imagens de forma inteligente, é preciso entender o conceito de domínio e suas possibilidades.
À primeira vista, ao trabalhar com imagens, durante a criação de sistemas e ferramentas de processamento de imagens, pensamos que será utilizado unicamente os pixels, menor elemento de uma imagem, como fonte de informação. Porém, os dispositivos de aquisição de imagem e técnicas de análise de imagem, permitem que os computadores vão muito além, que enxergar uma imagem apenas com suas cores.
Uma das várias formas que permitem os computadores enxergarem o mundo de forma diferente, é a representação de como disponibilizamos a informação para o computador, o domínio de uma função é uma destas formas.
Domínio de uma função, em matemática, nada mais é do que o conjunto de dados de entradas para uma função. Ou seja, uma função fornece uma saída de dados para cada conjunto de dados de entrada.
A seguir, são descritos os dois principais domínios de funções utilizados no processamento e análise de imagens: o domínio de espaço e domínio de frequência. Também é descrito o conceito de transformada, utilizada para intercambiar entre os domínios e alguns experimentos. Este artigo, tem como objetivo introduzir o usuário ao conceito de domínio de espaço e frequência, e nele não serão detalhadas características matemáticas.
Domínio de Espaço
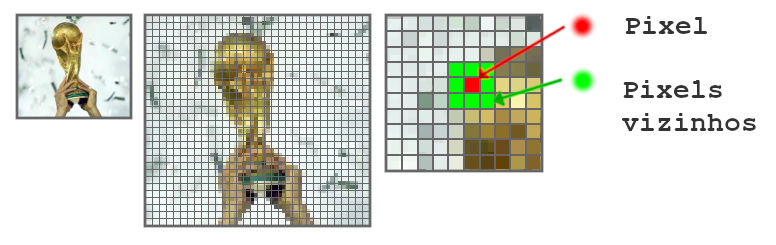
O domínio espacial refere-se a matriz de pixels da imagem digitalizada, geralmente contendo apenas as informações para reproduzir a imagem novamente em monitores. O pixel é a menor informação disponível em uma imagem (ver Fig 1).
Cada pixel, da imagem, geralmente contém as cores da imagem, mas também pode conter apenas sua representação em tons de cinza, ou até mesmo a informação multiespectral da imagem, como o espectro infravermelho, os raios gama e X, caso a câmera fotográfica consiga capturar essas informações.
Toda operação no domínio de espaço de uma imagem, utiliza a informação do pixel ou do pixel e seus vizinhos, para modificar a imagem. Em uma operação de adição de brilho, por exemplo, pode-se utilizar apenas a informação de um pixel de cada vez, para realçar o brilho da imagem, e em uma operação para esboçar (blur) é utilizada a informação do pixel e seus vizinhos. As funções de processamento de imagens no domínio espacial podem ser expressas como [MV]:
g(x,y) = T [ f(x,y) ]
Onde: g(x,y) é o pixel da imagem de saída (processada), f(x,y) o pixel da imagem de entrada e T é a função ou operador que opera sobre o pixel (x,y) e sua vizinhança.
As operações realizadas no domínio de espaço são denominadas de operações pontuais, operações locais e transformações geométricas. As operações geométricas não são descritas neste artigo.
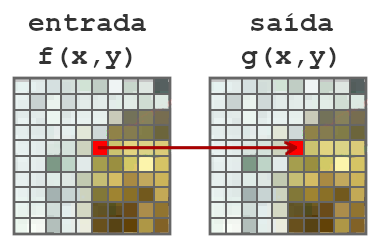
Operações pontuais
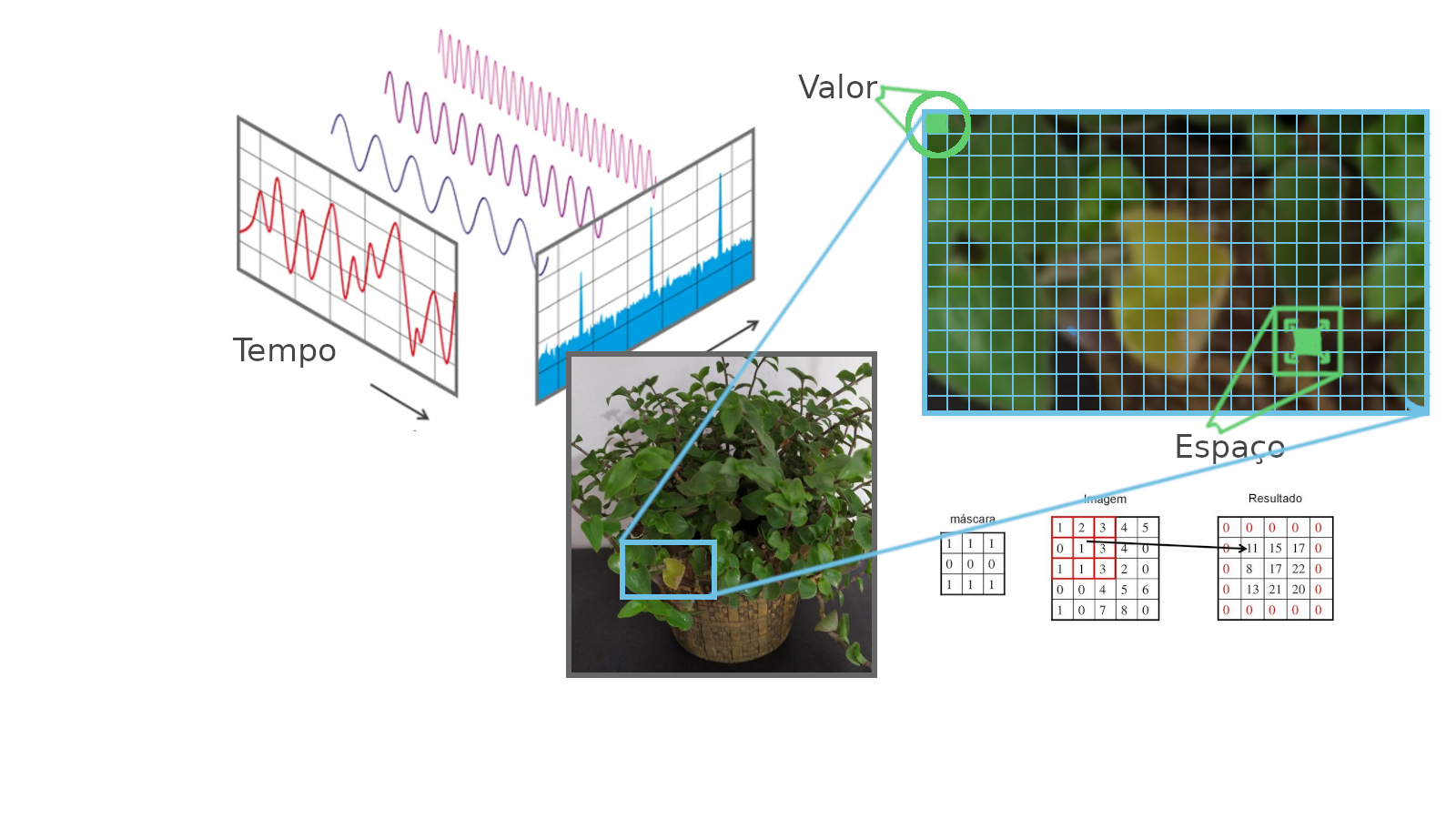
As operações pontuais utilizam apenas a informação (intensidade) de um único pixel como entrada de informação. Observe na Fig. 2 a área demarcada na imagem de entrada, em operações pontuais é utilizado apenas o pixel da posição (x,y) como entrada da operação que irá alterar o mesmo pixel da posição (x,y) na imagem de saída.
Operações básicas que modificam o contraste, o brilho ou a saturação são alguns exemplos de operações locais.
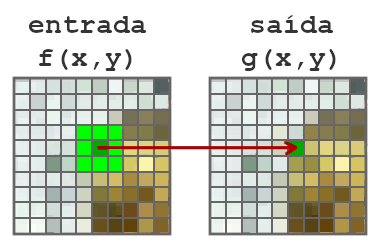
Operações locais
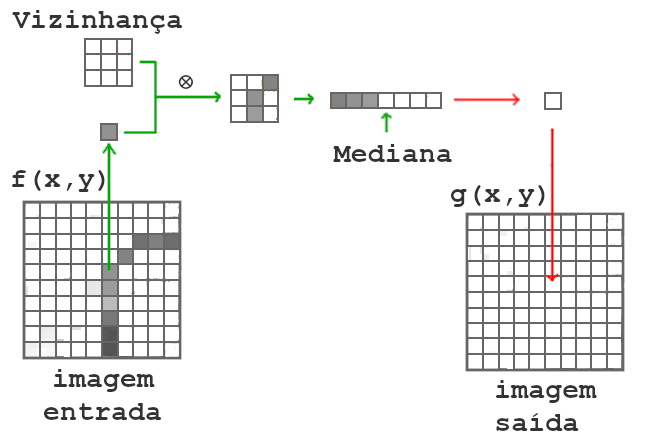
Em operações locais, o resultado de uma operação dependerá do valor do pixel de entrada e também dos seus pixels vizinhos. Observe na Fig. 3, que para gerar cada pixel g(x,y), destacado em verde, na imagem de saída a função recebe o mesmo pixel da imagem de entrada f(x,y) e também os seus pixels vizinhos.
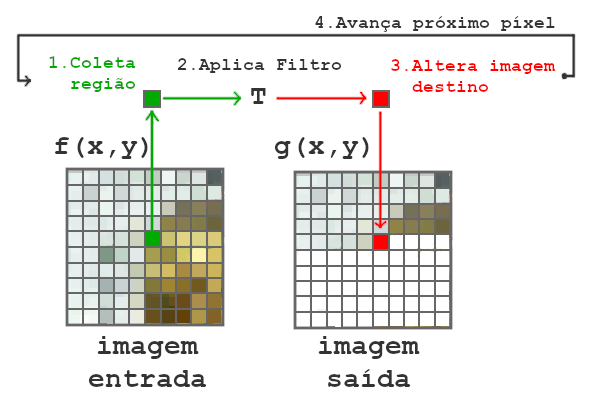
A seguir é apresentado o conceito de filtro espacial. A filtragem espacial é uma das principais ferramentas utilizadas em processamentos de imagens para uma ampla gama de aplicações, como suavização, nitidez, destaque e aperfeiçoamento de bordas. O filtro espacial consiste em realizar uma operação sobre os pixels da vizinhança e criar um novo pixel, com as coordenadas iguais às coordenadas do centro da vizinhança, e cujo valor é o resultado da operação de filtragem [GW]. O valor do pixel filtrado geralmente é atribuído à uma nova imagem, para não modificar a imagem original enquanto o filtro continua sendo realizado.
Na ilustração da Fig. 4 é demonstrado o funcionamento básico de um filtro no domínio espacial. Através de uma imagem de entrada é percorrido todos os pixels da imagem, informado uma coeficiente de entrada para o filtro, aplicado o filtro na posição do pixel de entrada e por fim devolvido o resultado do filtro na mesma posição do pixel de entrada em uma nova imagem.
Os filtros no domínio espacial são classificados de duas formas, filtros lineares e filtros não lineares. Os filtros também podem ser classificados como filtros passa-baixa e filtros passa-alta, em alusão aos filtros do domínio da frequência, melhor descritos na Seção Domínio de Frequência.
Filtros lineares
São considerados filtros lineares, os filtros que realizam operações lineares sobre os pixels da imagem [GW]. Em matemática um operador linear é uma transformação linear em um espaço vetorial (nele mesmo). O processo de filtragem linear é realizado por uma operação chamada de Convolução e Correlação.
Convolução e correlação espacial
A convolução e correlação são operações de vizinhança, em que cada pixel de saída é a soma ponderada dos pixels vizinhos de entrada por uma matriz de pesos. A matriz de pesos é chamada de núcleo (kernel) de convolução, também conhecido como filtro. O funcionamento da convolução e correlação são os mesmos, exceto que na convolução o primeiro filtro deve ser rotacionado a 180° [GW].
Conforme ilustrado na Fig. 5, o filtro linear realiza as seguintes etapas para calcular o pixel de saída da posição (6,5):
- Coleta o coeficiente de entrada(pixels vizinhos) do filtro;
- Gira o núcleo de correlação 180 graus sobre seu elemento central para criar um núcleo de convolução;
- Multiplica cada peso do núcleo de convolução pelo seus respectivos pixels de entrada;
- Soma os produtos individuais e aplica o resultado em uma imagem de saída.
No fim do processo, o filtro avança para o próximo pixel da imagem.
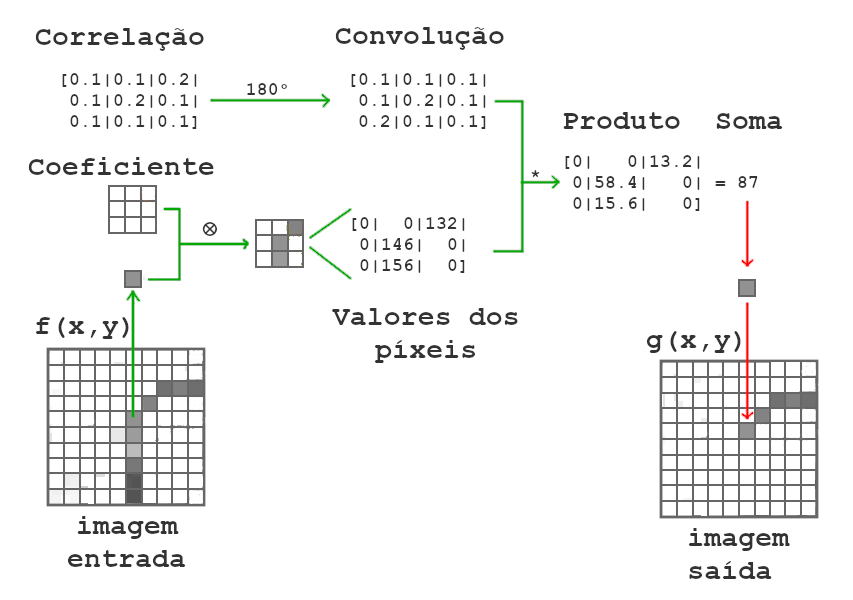
Ao realizar o filtro de convolução, com um núcleo superior ou igual a uma matriz 2×2, é preciso ajustar a imagem de saída, durante a filtragem, para que ela seja expandida com a quantidade de pixels iguais à quantidade de pixels adjacentes da posição central da imagem. Após a filtragem a imagem deve ser retraída ao seu tamanho original.
Na ilustração da Fig.6, são demonstradas as aplicações de dois filtros em sua forma discreta, o filtro gaussiano e o filtro Laplaciano, com núcleo de tamanho 3 x 3. O filtro gaussiano tem como característica, reduzir os ruídos das imagens e possui o efeito de borrão. O filtro Laplaciano destaca regiões de rápida mudança de intensidade, portanto, é frequentemente usado para detecção de bordas. Normalmente o filtro Laplaciano é utilizado após a imagem ser suavizada com outro filtro, como o gaussiano, nesta ilustração não foi utilizado esta suavização.

Importante ressaltar que você pode encontrar na literatura os termos filtro de convolução, máscara de convolução ou kernel de convolução. Como regra, esses termos são utilizados para expressar um filtro espacial, e não necessariamente o filtro para uma convolução. Da mesma forma a expressão “realizar a convolução de uma máscara” é utilizada para expressar o processo de deslocamento e soma dos produtos e não diferencia entre correlação e a convolução [GW].
Filtros não lineares
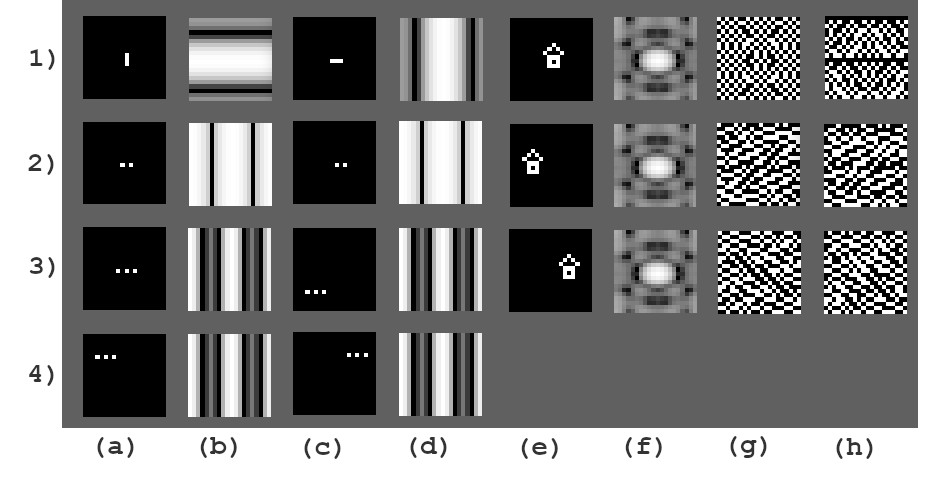
O que difere os filtros não lineares dos filtros lineares é que os valores dos pixels utilizados nesses filtros são combinados com alguma função não linear [BB]. Por exemplo: a função max, que coleta o pixel de maior intensidade em sua vizinhança; a função min que coleta o pixel de menor intensidade; as funções média, moda, mediana, entre outras. Uma forma de identificar alguns tipos de operações não lineares, é observar se nela existe alguma condição e uma ou mais variáveis locais mutáveis. Observe a função max, conforme ilustração da Fig. 7 , para ela identificar se determinado pixel é maior que outros de sua vizinhança, ela realiza uma condição de comparação entre os pixels vizinhos, onde compara 2 pixels e armazena o pixel de maior valor em uma variável local e depois utiliza esta variável para a próxima comparação, repetindo o processo até o último pixel da vizinhança, neste processo a variável local pode sofrer diversas alterações.
Outros exemplos de filtros não lineares são os filtros de gradiente Roberts e Sobel,para identificação de bordas em imagens. Os filtros não lineares identificam bordas, linhas, manchas e aplicam modificações sem se preocupar com níveis de cinza da imagem de origem.
Domínio de Valor
Utilizado apenas para referenciar o pixel da imagem ou a menor informação útil da imagem. O Domínio de valor nada mais é que uma expressão, não um domínio, para relacionar funções que utilizam apenas um pixel para realizar operações aritméticas na imagem. Por exemplo, uma operação de adição ou subtração que modifica um pixel de cada vez, sem utilizar as informações de seus pixels vizinhos.
Transformada
Em matemática, uma transformação é uma função f (geralmente com algum suporte geométrico) que mapeia um conjunto X para si mesmo f : X → X. Os exemplos incluem transformações lineares de espaços vetoriais e transformações geométricas, que incluem transformações projetivas, transformações afins e transformações afins específicas, como rotações, reflexos e translações [GW]. A transformada resulta na alteração da representação inicial da imagem, de modo a prover informações que permitam analisar a imagem de outra forma [PS].
A transformada espacial de vetores, altera o domínio de uma função para outro tipo de domínio, resultando em uma nova forma de representar os valores dos vetores. Um exemplo de transformada é a transformada de Fourier que consiste em transformar a representação da imagem no domínio espacial para o domínio da frequência. A seguir, é apresentado superficialmente esta transformada e também como aplicar filtros no domínio da frequência.
Domínio de Frequência
Em 1822, o matemático francês Hean Baptiste Joseph Fourier publica em seu livro “A teoria analítica do calor”, contribuição pela qual ele é mais lembrado. Fourier, neste livro, afirma que qualquer função periódica pode ser expressa como a soma de senos e/ou cossenos de diferentes frequências, cada uma multiplicada por um coeficiente diferente [GW]. A transformada de Fourier, tem como objetivo a transformação de um sinal (função) do domínio do espaço para o domínio de frequência [GW]. Essa transformada foi utilizada inicialmente no processamento de sinais e em funções unidimensionais. Posteriormente, sua versão 2D, prevê informações a respeito das intensidades de cinza, ou um espectro de cor, e passou a ser utilizada no processamento e análise de imagens [PS].
Em processamento de imagens, o domínio da frequência representa a variação de intensidade entre os pixels. Em um cenário em que um pixel tenha a cor branca (alta intensidade) e seus vizinhos sejam pretos (baixa intensidade), a relação de frequência deste pixel branco em relação aos pixels pretos é tido como alta, pois suas intensidades são distantes entre si. Por outro lado, para um pixel cuja intensidade seja relativamente baixa, cinza escuro, e seus pixels vizinhos sejam de cor preta, a relação de frequência destes é baixa.
Na ilustração da Fig. 7, é demonstrado os espectros de magnitude após realizar a transformada de Fourier (através da função DFT) das imagens de entrada. Observe nesta ilustração, que as figuras 2a e 2b, as figuras 3a, 3c, 4a e 4c, e as figuras 1e, 2e e 3e possuem exatamente o mesmo espectro de magnitude. Isto ocorre, porque independente da localização dos pixels na imagem, eles possuem a mesma variação de intensidade em relação aos seus vizinhos. Este espectro é um das características da transformada de Fourier.
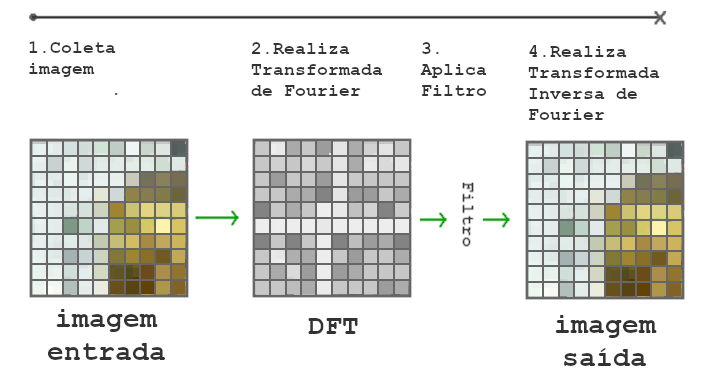
Os filtros no domínio da frequência são realizados de uma forma bem simples, que consiste em realizar a transformada de Fourier, aplicar o filtro e realizar a transformada inversa de Fourier, conforme ilustra a Fig. 8.
As baixas frequências na transformada, são relacionadas a componentes com variação de intensidade lenta (suave), como paredes de uma sala, por exemplo. Por outro lado, altas frequências são relacionadas a ruídos e bordas. Desta forma, um filtro que deixe passar baixas frequências, possui o efeito de borrar a imagem e um filtro que deixe passar altas frequências possui o efeito de realçar detalhes abruptos e provocaria uma redução do contraste da imagem [GW]. A seguir, são melhor detalhados estes filtros.
Filtro de Passa Baixa
O efeito de um filtro passa-baixa é o de suavização de imagem, uma vez que as frequências altas que correspondem às transições abruptas são reduzidas. A suavização tende a diminuir o efeito de ruídos na imagem, que possuem uma alta variação de intensidade e serão ignorados pelo filtro, porém o filtro causa o efeito de borramento e pode resultar na perda de detalhes finos [PS].
Para entender o efeito dos filtros passa-baixa, observe a ilustração da Fig. 9. Nela foi realizada a transformada da imagem (a) do domínio de espaço para o domínio da frequência, utilizando a função DFT (Discrete Fourier Transforms – Transformada discreta de Fourier). Após a transformação, note que no centro da imagem (b) estão contidas as informações das baixas frequências da imagem em seu domínio espacial. Ao realizarmos um corte e mantermos apenas as informações centrais no domínio da frequência, conforme imagem (c), estaremos mantendo apenas as informações de baixa frequência da imagem.

Filtro de Passa Alta
O filtro passa alta pode ser entendido como uma operação inversa ao passa baixa e são normalmente usados para realçar os detalhes na imagem. É um filtro que permite a passagem de frequências altas e reduz a amplitude de frequências baixas. Observe na Figura 10, os efeitos produzidos ao manter apenas as altas frequências das imagens originais (a). A imagem final (c) destacou as bordas dos objetos, este efeito ocorre porque é na alta frequência que estão armazenados os maiores detalhes das imagens.

Nos exemplos das ilustrações Fig. 10, 11 e 12 são demostrados alguns efeitos ao aplicar determinado núcleo de convolução diretamente no filtro de domínio da frequência e posteriormente mesclado a imagem resultante com a imagem de entrada. Clique nas ilustrações para ampliá-las.



Outros tipos de Domínios
Além destes domínios descritos neste artigo, existem outros tipos de transformadas conhecidas que alteram o domínio da imagem, como por exemplo:
- A transformada discreta de Hartley, proposta em 1942 por Hartley, que possui propriedades semelhantes a transformada de Fourier e necessita de computação real (hipotéticas máquinas de computação que usam números reais com precisão infinita). Aproximadamente 40 anos depois, Bracewell propôs uma versão discreta denominada DHT. A DHT começou a despertar o interesse da comunidade de processamento de sinais [PS].
- A transformada de Hough (HT) desenvolvida por Paul Hough em 1962 é um método para detecção de formas que são facilmente parametrizadas (linhas, círculos, elipses, etc.) em imagens computacionais.
- Transformada Wavelet foi apresentada em 1909 por Haar e é muito utilizado na compressão de imagens.
Comentários finais
Uma das melhores formas de entender melhor os efeitos destes domínios é testando operações e funções que alteram a imagem, pois uma mesma operações pode produzir diversos efeitos diferentes depentendo da imagem de entrada utilizada.
O domínio da frequência, tem a natureza mais complexa, porém, ele é fundamental para quem tem como objetivo trabalhar com processamento de imagens e não necessariamente com visão computacional, pois trabalhar com processamento de imagens, requer mais cuidados com a qualidade final da imagem e entender este domínio pode auxiliar na aplicação de filtros, técnicas de compreensão e redimensionamento de imagem.
O domínio de espaço, com sua natureza mais simples, possui a maior quantidade de funções, operações e técnicas de imagens, porque ele representa a imagem em si. Este domínio, deve ser completamente entendido, para trabalhar com qualquer foco na área de visão computacional e processamento de imagens.
Espero que o post possa ter o ajudado. Deixe seu comentário e dúvidas abaixo.
Source:
https://github.com/visaocomputacionalexemplos/dominiovalorespfreq
Referencias:
[BB] BURGER, W.; BURGER, M. J. Digital Image Processing: An Algorithmic Introduction Using Java, Springer, 2005
[GW] GONZALEZ, R. C., WOODS, R. E. Processamento de Imagens Digitais.
Editora Edgard Blucher, ISBN 978-85-8143-586-2, 3 ed., São Paulo, 2010
[MV] MARQUES FILHO, O.; VIEIRA NETO, H. Processamento Digital de Imagens, Rio de Janeiro:Brasport, 1999
[GM] GANYUSHKIN, O; MAZORCHUK, V. Classical Finite Transformation Semigroups: An Introduction. Springer Science & Business Media, 2008
[PS] Pedrini, H.; Schwartz, W. R.; Análise de Imagens Digitais: Princípios, Algoritmos e Aplicações. Thomson Learning, 2007

Nenhum comentário ainda!