A palavra Morfologia é originalmente um ramo da biologia, que estuda as formas e estruturas dos animais e plantas. Utilizamos esta palavra no contexto de Morfologia Matemática, como um instrumento para extração de componentes da imagem, que sejam úteis para representação e descrição da forma de uma região, como fronteiras, esqueletos, realce, filtragem, segmentação ou esqueletização [GW].
A morfologia também pode ser utilizada para extração de componentes conexos, busca de padrões específicos na imagem, delimitação de fecho convexo, extração de bordas entre outros [PS].
Neste post é apresentado um resumo sobre morfologia matemática, sem detalhar suas fórmulas matemáticas.
Imagem Digital e Binária
Uma imagem digital é formada por uma quantidade finita de amostras de uma cena, capturada pela lente de uma câmera, também pode ser chamada de imagem discreta e é representada como subconjunto do plano cartesiano Z2, onde Z representa o conjunto dos números inteiros. Cada amostra da imagem, conhecida como pixel, está localizada em uma coordenada (x, y) da imagem, associada alguma informação sobre a cor [VL].
Uma imagem binária é composta por dois tipos de pixels, os do plano de fundo e o plano principal, que são representados normalmente usando preto e branco, ou 0 e 1, respectivamente [VL]. Normalmente representam a área de interesse durante o processamento morfológico.
Neste artigo é apresentada a morfologia matemática binária (em imagens binárias).
Elemento Estruturante
Um conceito importante na morfologia matemática é a definição de elemento estruturante, também chamado de núcleo. O elemento estruturante é um vetor bidimensional pré-definido, representado por zeros (0) e uns (1), com uma coordenada indicando o centro da operação e pode assumir diversas formas e aspectos, dependendo do tipo de efeito desejado a ser aplicado na imagem.
A seguir, são demonstrados 3 diferentes vetores de elementos estruturantes e suas imagens representativas, com o centro de operação destacado em vermelho.
[1, 1, 1,
1, 1, 1,
1, 1, 1]

[0, 1, 0,
1, 1, 1,
0, 1, 0]

[1,
1,
1]

A ideia básica da morfologia binária é sondar uma imagem com o elemento estruturante pré-definido, analisando como essa forma se encaixa ou não nas formas da imagem.
Erosão e Dilatação
A erosão e a dilatação são dois operadores fundamentais em Morfologia Matemática, muitos operadores morfológicos mais sofisticados se baseiam nestas duas operações.
Erosão
Símbolo / Representação : ⊖
Definição: A ⊖ B = { z | (B)z ∩ Ac = ∅ }
A erosão consiste em testar se o elemento estruturante se encaixa na imagem de origem, gerando uma nova imagem de destino, onde cada teste realizado com sucesso, é identificado na imagem de destino com o valor 1 e identificado com o valor 0 caso a estrutura não tenha sido localizada. Os valores 0 e 1 podem ser substituídos por outros valores, caso necessário.
O efeito prático do processo morfológico chamado erosão, consiste na modificação das feições da imagem, diminuindo-as em seu entorno, literalmente “erodindo-as” [MM].
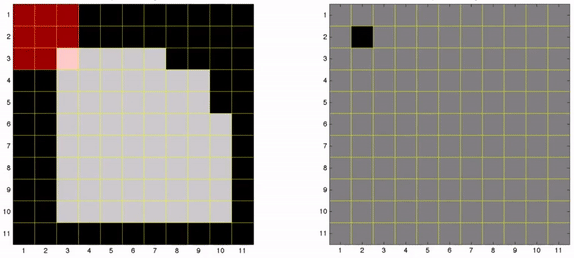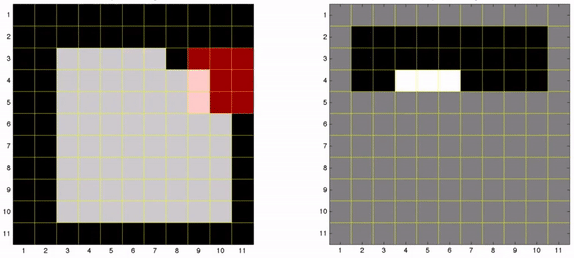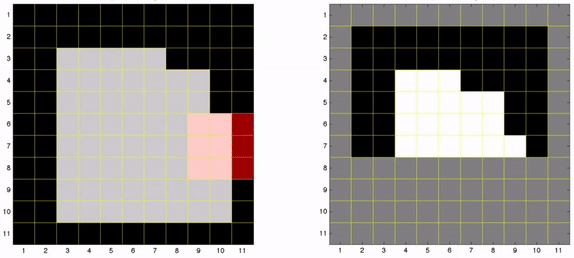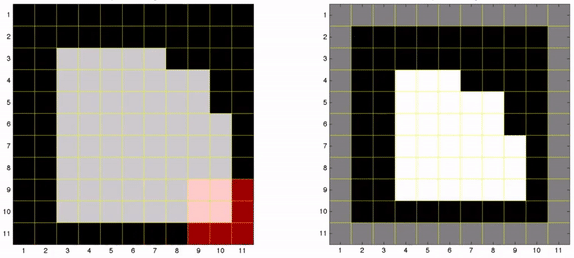
Observe na ilustração a seguir, o passo a passo da erosão da imagem, de tamanho 11×11, pelo elemento estruturante, de tamanho 3×3. O processo inicia pelo teste do elemento estruturante na parte superior esquerda da imagem, onde é verificado se cada elemento do núcleo é encontrado da imagem. Para isso, é verificado se cada um dos elementos [1, 2, 3, 4, 5, 6, 7, 8, 9] do núcleo estão contidos nos elementos de coordenada [(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)] da imagem, e registrado o valor 1 (branco) na imagem de destino caso todos os elementos sejam encontrados, como o teste não passou, na imagem de destino é registrado o valor 0 (preto). Então, é deslocado a verificação do núcleo para os próximos elementos da imagem, até que todos sejam testados.

(Núcleo)
A seguir, na ilustração da Fig. 6, é exibido um exemplo de erosão morfológica de uma imagem de placa de circuitos. Neste exemplo vamos tentar remover todos os circuitos e manter apenas suas extremidades. O primeiro processo realizado, consiste em carregar a imagem, convertê-la em tons de cinza e realizar a limiarização, para termos uma imagem em preto e branco (zeros e uns). Com a imagem limiarizada foi realizada a sua Erosão, com uma matriz 3×3 de valores 1.
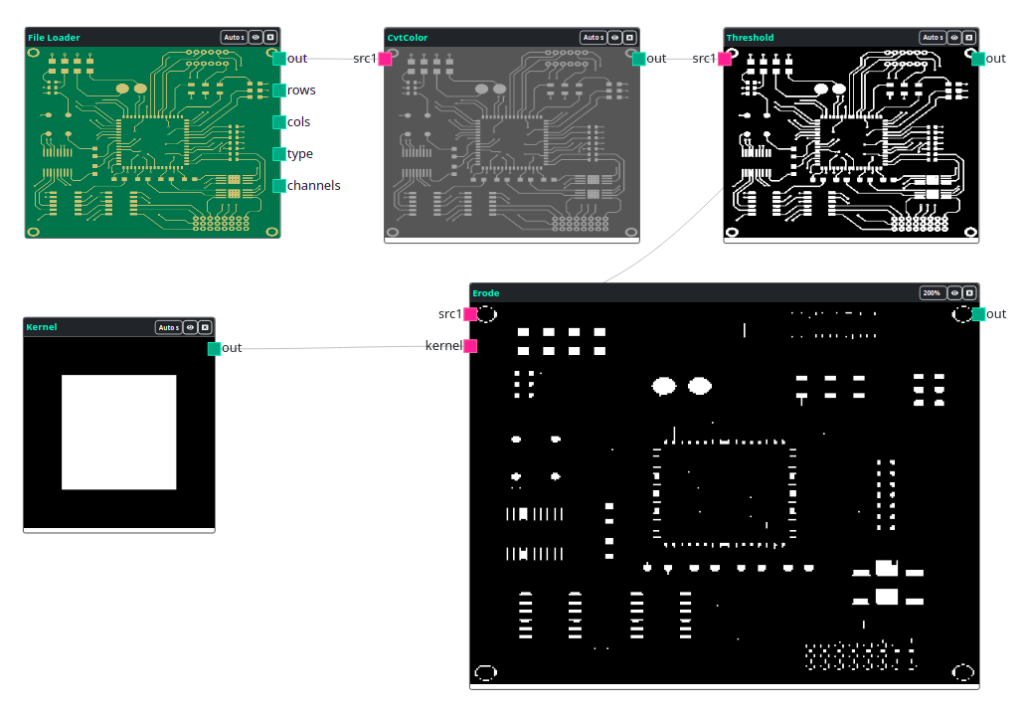
Podemos observar pela imagem, que este simples processo eliminou todos os traços/linhas da imagem de entrada, mantendo apenas as estruturas maiores. O resultado não foi uma extração ideal de estrutura, porém, com uma única aplicação de operação morfológica foi possível remover muitas informações indesejadas. O exemplo acima foi realizado utilizando a ferramenta online OpenCV-Flow.
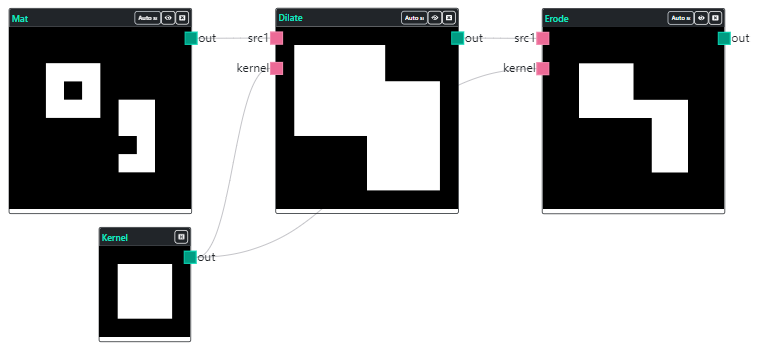
Dilatação
Símbolo / Representação: ⊕
Definição: A ⊕ B = { z | (^B)z ∩ A ≠ ∅ }
A dilatação, de certa forma, é o contraponto da erosão. Ela consiste em testar cada elemento da imagem de origem e verificar se possui valor 1, caso exista na imagem de destino, então é adicionado os valores do elemento estruturante a partir da posição central do elemento estruturante.
O efeito prático do processo morfológico chamado Dilatação consiste na modificação das feições da imagem, aumentando-as em seu entorno [MM].
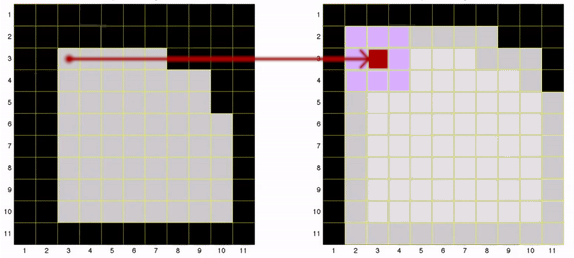
Observe na ilustração a seguir, o resultado da aplicação do elemento estruturante (núcleo) na imagem. O núcleo de forma quadrada, com tamanho 3×3, possui os valores [1,1,1,1,1,1,1,1,1] e centro de coordenada (2,2). Note que ao aplicar o núcleo na coordenada (3,3) da imagem de entrada, resultou na imagem de saída a expansão daquele ponto, ao aplicar/copiar o elemento estruturante na imagem de saída. Todo o processo é repetido para cada elemento da imagem.

(Núcleo)
Abertura e Fechamento
Duas outras operações morfológicas importantes são a abertura e fechamento.
Abertura
Símbolo / Representação: ◦
Definição: A ◦ B = (A ⊖ B) ⊕ B
A abertura de uma imagem A por um elemento estruturante B é simplesmente a operação de erosão de A por B, seguida da dilatação de A por B [PS].
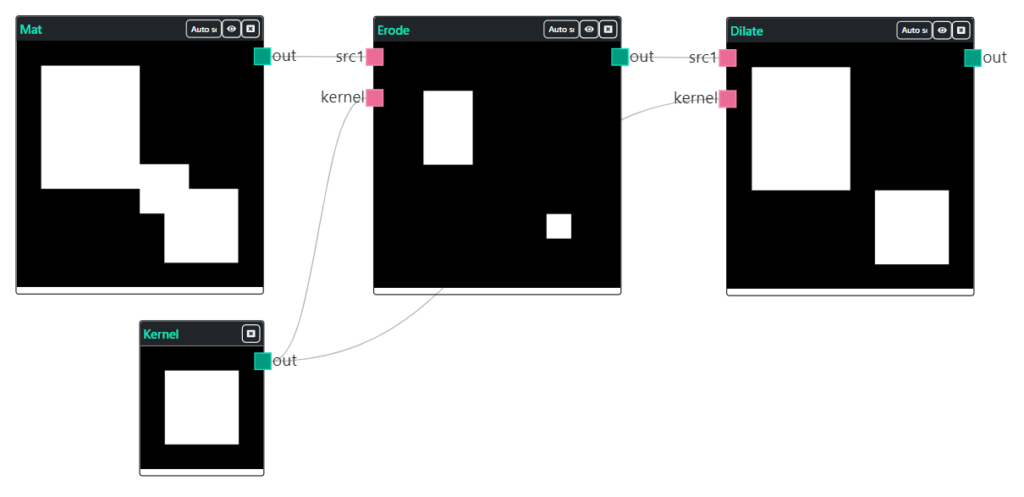
Ao realizar a erosão seguida da dilatação, o efeito produzido na imagem é de abertura de pontos/ligações e remoção de ruídos. Observe na ilustração da Fig. 9, que após realizar a operação de erosão na imagem, a conexão que existia entre os retângulos foi perdida e também foram reduzidos seu tamanhos. Porém, ao aplicar a dilatação esses retângulos voltaram a ter sua forma inicial.
Fechamento
Símbolo / Representação: •
Definição: A • B = (A ⊕ B) ⊖ B
O fechamento de uma imagem A por um elemento estruturante B é simplesmente a operação de dilatação de A por B, seguida da erosão de A por B [PS] .
Ao realizar a dilatação seguida da erosão, o efeito produzido na imagem são o fechamento de pequenos buracos e criação de conexões. Observe na ilustração da Fig. 10, que após realizar a dilatação, com a espação dos elementos, os buracos iniciais foram fechados, e com a realização da erosão o componente voltou a ter o aspecto da sua estrutura inicial, com os pequenos buracos fechados. Porém, como consequência desta técnica os componentes que estavam próximos se conectaram.
Filtragem morfológica
As operações morfológicas podem ser utilizadas como filtros de imagem, como filtros espaciais apresentados no artigo Domínios de Valor, Espaço e Frequência.
A ilustração da Fig. 11 mostra uma imagem de impressão digital corrompida por ruído, no topo a esquerda, sendo que o ruído se manifesta como elementos aleatórios claros sobre o fundo escuro e como elementos escuros sobre componentes claros na digital. O objetivo é eliminar todos os ruídos sem danificar a estrutura da digital [GW].
A seguir, na ilustração da Fig. 11, um exemplo de filtragem utilizando abertura seguida do fechamento morfológico, utilizando um elemento estruturante em forma de cruz.
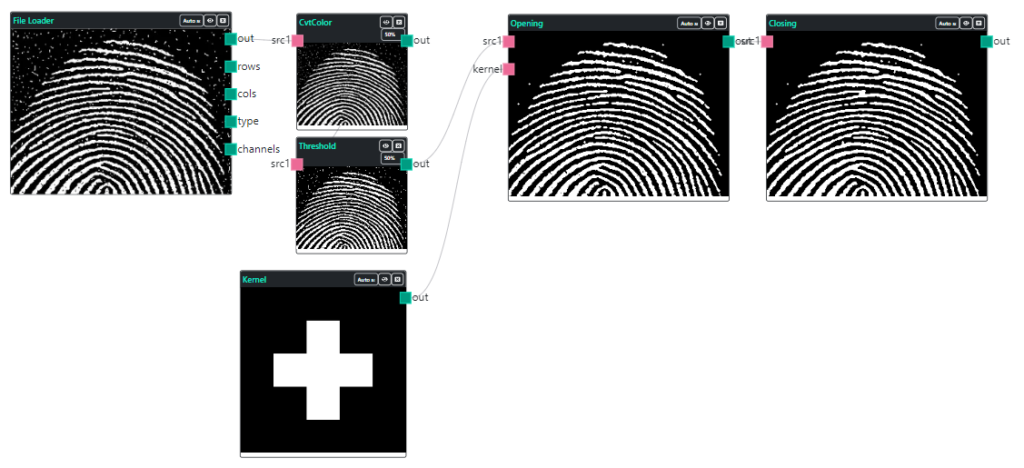
O resultado final, após o fechamento, esta quase sem ruídos, mas com algumas das cristas de impressão não totalmente reparadas e também apresenta algumas quebras, além de que algumas cristas foram conectadas e não deveriam. Isto não é inesperado utilizando esta técnica e para resolver esta situação seria necessário aplicar outras técnicas de processamento de imagens, que talvez resolveriam o problema, como realizar afinamento ou esqueletização.
Estes conceitos apresentados neste artigo são a base da morfologia matemática. Ela possui muitas outras técnicas, como extração de fronteiras, transformada acerto-ou-erro, afinamento, esqueletização, poda e extração de componentes conexos.
Referências:
[GW] GONZALEZ, R. C., WOODS, R. E. Processamento de Imagens Digitais. Editora Edgard Blucher, ISBN 978-85-8143-586-2, 3 ed., São Paulo, 2010
[PS] Pedrini, H.; Schwartz, W. R.; Análise de Imagens Digitais: Princípios, Algoritmos e Aplicações. Thomson Learning, 2007
[VL] Visual-Lab – Instituto de computação. Morfologia Matemática em Análise de Imagens. Acessado em 30/01/2023.
[MM] Matosak, B. M.; Medeiros, N. G; IMGedu – Capítulo 3 Morfologia Matemática. Acessado em 30/01/2023.